































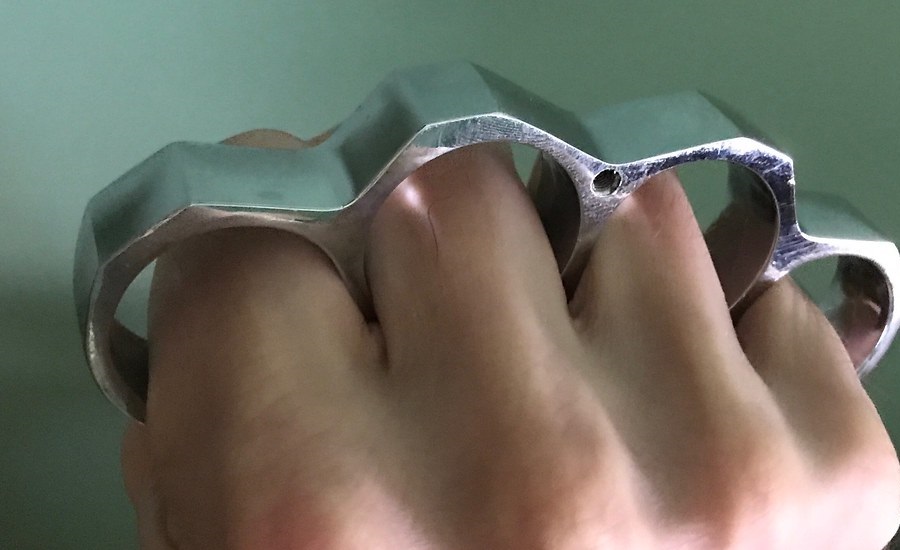
















PARACORD WRAPPED KNUCKLE DUSTER – KNIVESINDIA
trigger finger
Description
PARACORD WRAPPED KNUCKLE DUSTER – KNIVESINDIA
Information Of Products
- Category
- BrandKNUCKLE
- Commodity ConditionThere is no noticeable scratches or dirt
- Shipping ChargesShipping included (paid by seller)
- Shipping MethodEasy Mercari shipping
- Days To ShipShips in 1-2 days
www.avvascookbook.com
Meet the seller

e73459
Identity Confirmed
Speed Shipping
This seller ships within 24 hours on average
Comment (28)

09308a
Black Plastic Knuckle Duster - Nonmetal Black Knuckles ...

10pcs Antique Brass Knuckle Duster Charms Pendants Connector Jewellery Making X122 (NOT ACTUAL WEAPON)

Solid Brass Knuckle Duster - Real Brass Knuckles - Classic Brass ...

Outdoor Fitness Metal Brass Knuckle Duster Self-defense Boxing ...

KNUCKLE DUSTER - Watchdog Tactical

Stainless Steel Knuckle Duster Paperweight – Cakra EDC Gadgets

YOU'RE NEVER ALONE KNUCKLE DUSTER – CHRISHABANA

JEWELLERY - OR A $10,000 KNUCKLE DUSTER? -

Zinc Alloy Brass Knuckle Duster 154g Heavy Duty Self Defense Tool ...

Solid Brass Knuckle Duster - Self-Defense Brass Knuckles - Classic ...

Lot - DOLNE APACHE KNUCKLE DUSTER

Japanese Original Design Medium Brass Knuckle Duster Charm Made ...

Pocket Slim Spiked knuckleduster - Rajput Knife

Black Heavy Duty Thick Knuckle Duster for Travellers Riders Self ...

Knuckle Duster (Rubber)

Johnny T's - Knuckle Duster - SAX Tees – SAXTEES

Stainless Steel 316 Knuckles / Knuckle Duster with Cubic Zirconia Pendant

Knuckle duster, England, 1914-1918 | Science Museum Group Collection

Make a Knuckle Duster or Brass Knuckles (Reupload) - YouTube

Silver Black Metal Knuckle Duster Four Finger Self Defense Tools ...

Knuckle Dusters

Knuckle dusters or nah for self defense? : r/martialarts

Black Iron Knuckle Duster

Knuckle duster black large standard

Solid Steel Knuckle Duster Brass Knuckle - BLACK AND GREY ...

Metal Fight Knuckle Duster Four Finger Martial Arts Fighting Iron ...

A Basic Guide to Knuckle Dusters for the Newbies! | by Sophia Zara ...

Real 304 Stainless Steel Knuckle Dusters Self Defense – Cakra EDC ...

Other items
-

$17$14.99PARACORD WRAPPED KNUCKLE DUSTER – KNIVESINDIA -

$16$13.99Boxer Knuckle duster - Aluminium or Brass Couleur Grey -

$19$15.99Does anyone know any places where you could buy knuckle knives ... -
$23$18.99Brass knuckles And knives... - Brass knuckles And knives -

$24$19.99Are Brass Knuckles Illegal in NJ? | Brass Knuckles Weapons Charge ... -

$21$16.99Are Brass Knuckles Legal in Canada? -

$14$10.99Knuckle - Wikipedia -
$23$17.99Knuckle pads -

$15$11.99Are Brass Knuckles Legal? - Firearms Legal Protection -

$17$12.99Is It Legal to Own Brass Knuckles in Connecticut? -

$20$14.9910pcs Antique Brass Knuckle Duster Charms Pendants Connector Jewellery Making X122 (NOT ACTUAL WEAPON) -

$19$13.99Brass Knuckles Bring the Pain Tattoo Art T-Shirt -

$22$15.9910pcs Antique Brass Knuckle Duster Charms Pendants Connector Jewellery Making X122 (NOT ACTUAL WEAPON) -

$26$18.99A Proper Way To Hold And Use Brass Knuckles | by Jairus Nadab | Medium -

$28$19.99The History Around Brass Knuckles | Brass Knuckles Knife | Knucks -

$24$16.99ZS650BK: Black Brass Knuckles -
$16$10.99Brass knuckles victim confronts her attacker -

$26$17.99Teen Charged in Brass Knuckles Battery Case Deemed Fit to Stand Trial -

$18$11.99Does anyone know any places where you could buy knuckle knives ... -

$19$12.99Original U.S. Vietnam War Private Purchase Parsons “M-7” Brass ...

